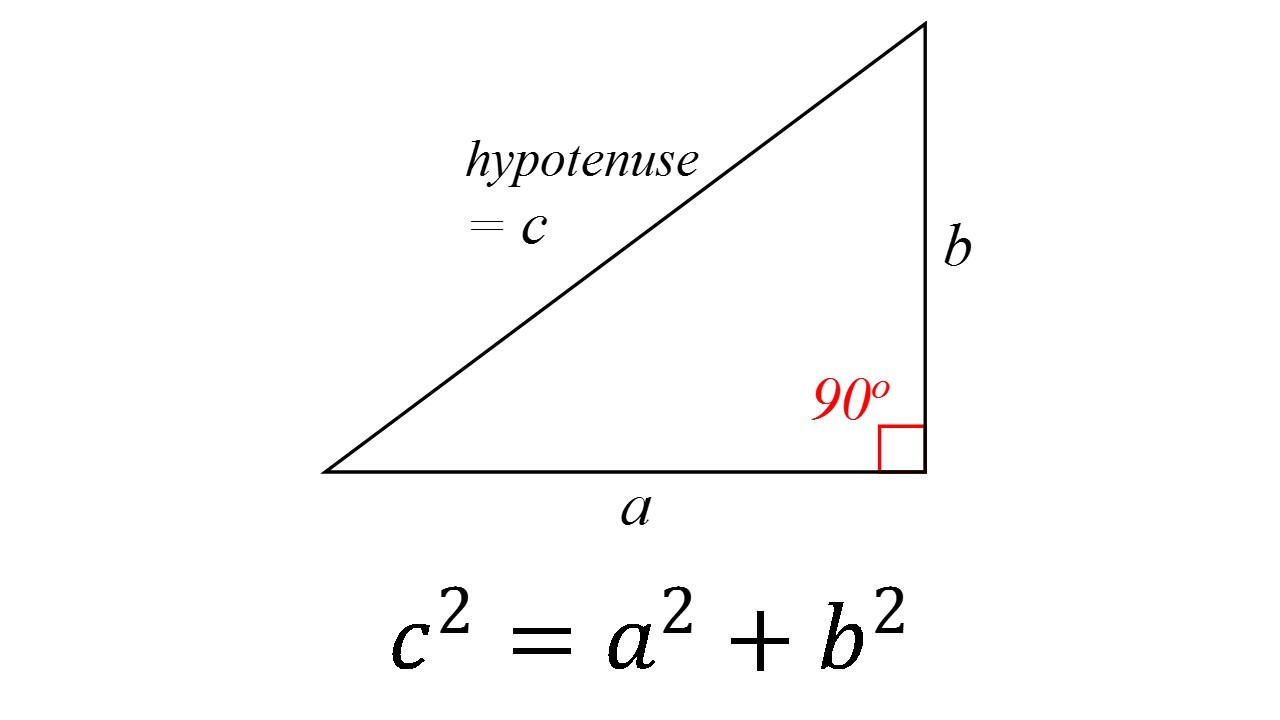
How do you use the Pythagorean Theorem to determine if the
4.6 (257) In stock

4.6 (257) In stock
c^2 != a^2 + b^2, therefore, this cannot be a right triangle. The Pythagorean Theorem applies to right angle triangles, where the sides a and b are those which intersect at right angle. The third side, the hypotenuse, is then c To test whether the given lengths of sides create a right triangle, we need to substitute them into the Pythagorean Theorem - if it works out then it is a right angle triangle: c^2 = a^2 + b^2 15^2 != 5^2+10^2 225 != 25+100 225 != 125 In reality, if a=5 and b=10 then c would have to be c^2 = 125 c =sqrt(125) = 5sqrt(5)~= 11.2 which is smaller than the proposed value in the question. Therefore, this cannot be a right triangle.

How to Find the Area of a Right Triangle Using the Pythagorean Theorem, Geometry

Apply the Pythagorean theorem. Find whether the given triangle has a right angle.

4 Ways to Solve Pythagoras Theorem Questions - wikiHow

Pythagorean Triples - Definition, Formula, Examples

Converse of Pythagorean Theorem - Expii

How to Determine Whether a Triangle is a RIGHT Triangle
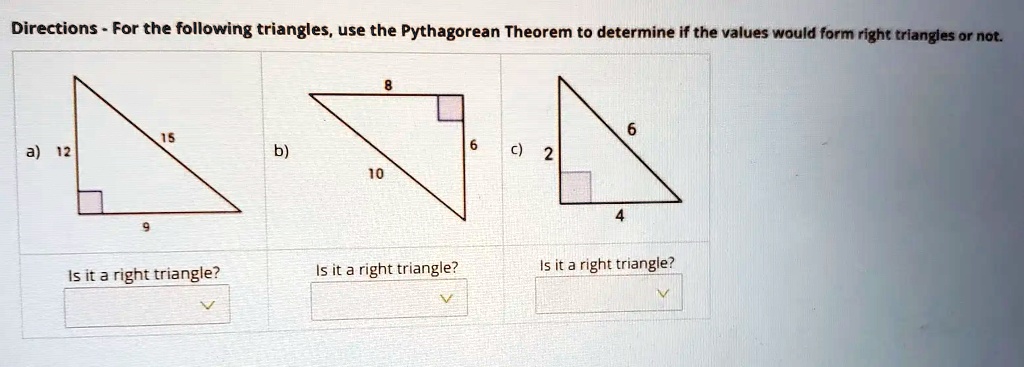
SOLVED: Directions For the following triangles, use the Pythagorean Theorem to determine if the values would form right triangles or not Is ifa right triangle? Is it a right triangle? Is II
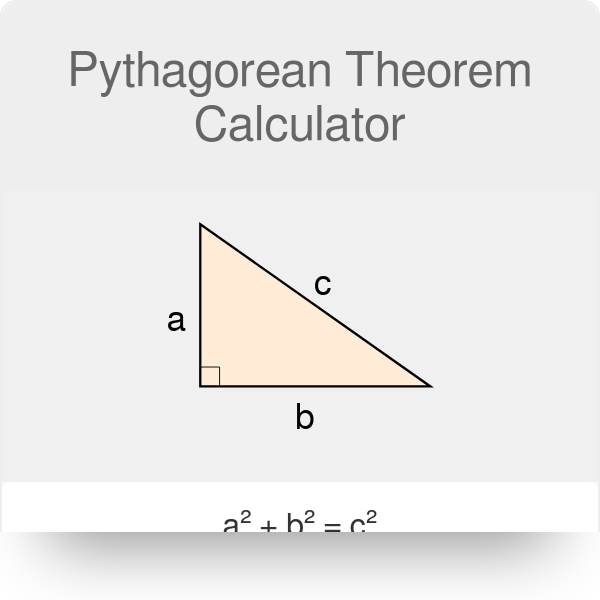
Pythagorean Theorem Calculator

How do you use the Pythagorean Theorem to determine if the following three numbers could represent the measures of the sides of a right triangle: 20, 6, 21?

How to Use the Pythagorean Theorem: 12 Steps (with Pictures)
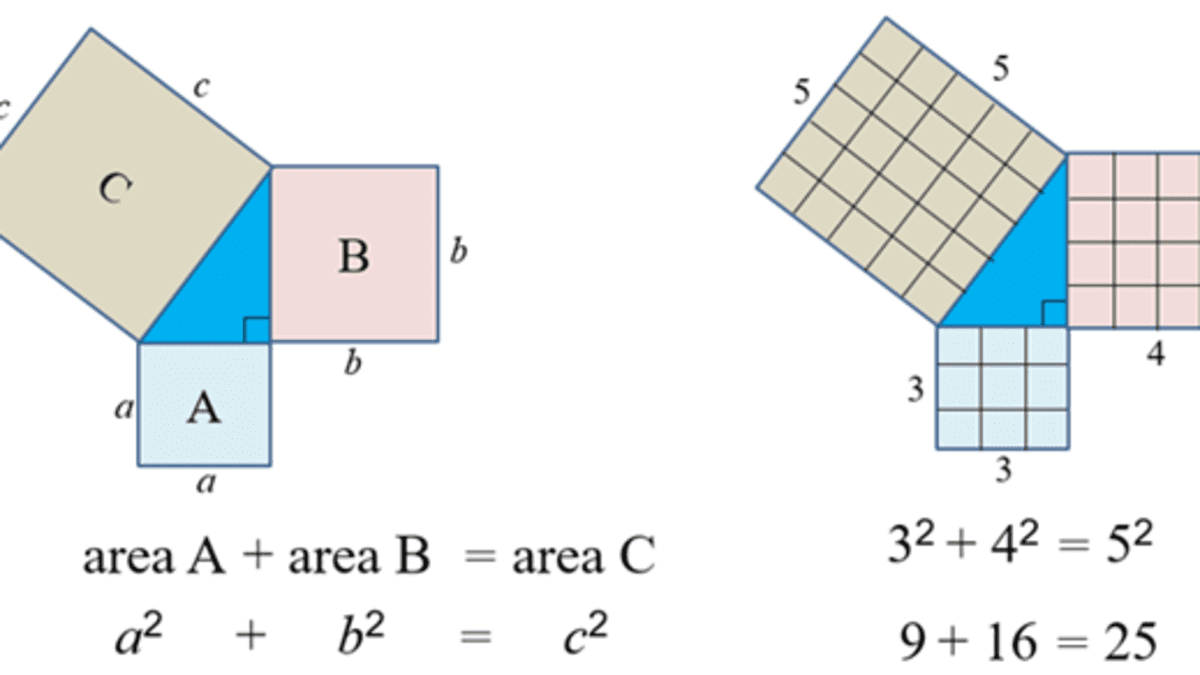
Pythagoras' Theorem Using Polygons, Circles and Solids - Owlcation
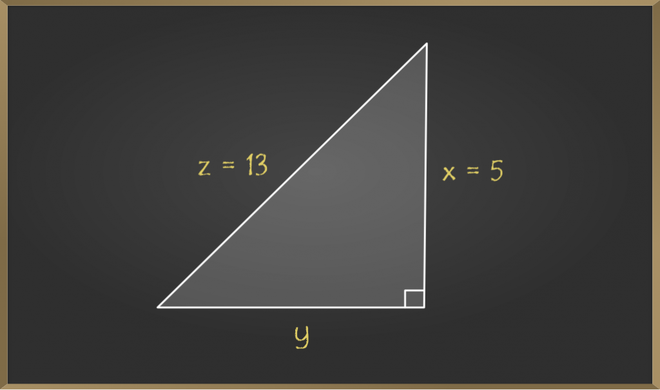
Pythagoras Theorem Formula, Proof, Examples and Applications

How to Use the Pythagorean Theorem: 12 Steps (with Pictures)
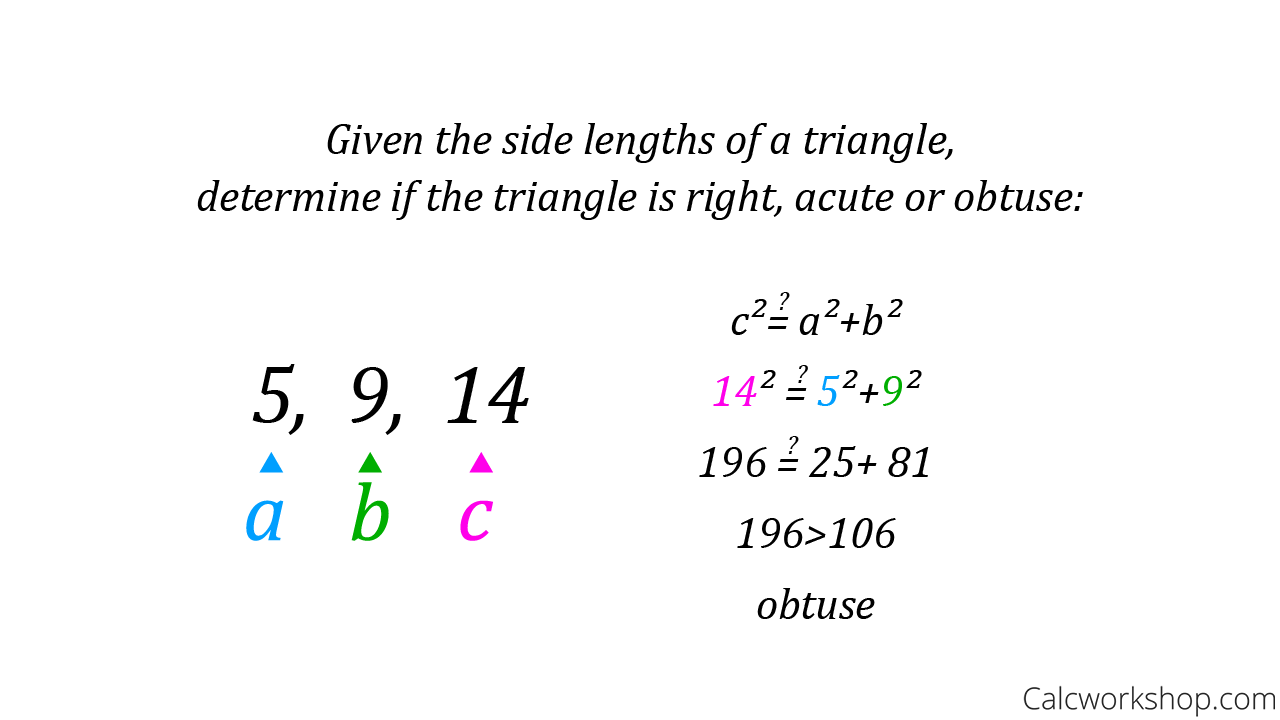
Converse of the Pythagorean Theorem Explained (2019)

Lesson Explainer: Applications on the Pythagorean Theorem